Newton's Law of Gravitation.

NEWTON'S LAW OF GRAVITAION

 নিউটনের মহাকর্ষ সূত্র

আলোচ্য বিষয় :-

i)নিউটনের মহাকর্ষ সূত্র      

ii)মহাকর্ষীয় ধ্রুবকের সংজ্ঞা 

iii)মহাকর্ষীয় ধ্রুবকের i)একক ii)মান ও iii)মাত্রা

iv)মহাকর্ষীয় ধ্রুবক এবং অভিকর্ষজ ত্বরণের মধ্যে সম্পর্ক প্রতিষ্ঠা 

v)অভিকর্ষজ ত্বরণ ও পৃথিবীর গড় ঘনত্বের মধ্যে সম্পর্ক  প্রতিষ্ঠা কর। 

1)নিউটনের মহাকর্ষ সূত্রটি বিবৃত কর। এই সূত্র থেকে মহাকর্ষীয় ধ্রুবকের সংজ্ঞা দাও ।

মহাবিশ্বের যে কোনো দুটি বস্তুকণা তাদের কেন্দ্রের সংযোগকারী সরলরেখা বরাবর পরস্পরকে আকর্ষণ করে ।এই আকর্ষক বলের মান বস্তু দুটির ভরের গুণফলের সমানুপাতিক এবং ওদের মধ্যকার দূরত্বের বর্গের ব্যস্তানুপাতিক ।

মনেকরি m₁ ও m₂  ভরের দুটি বস্তুকণা পরস্পর r দূরত্বে অবস্থিত ।বস্তু দুটি পরস্পরের উপর  F বল প্রয়োগ করলে নিউটনের মহাকর্ষ সূত্র অনুসারে,

\(F\propto{m_1m_2}\)

\(F\propto{\frac{1}{r^2}}\)

\(F\propto\frac{{m_1m_2}}{r^2}\)

\(F=G\frac{{m_1m_2}}{r^2}\)........i)

  G একটি ধ্রুবক। এই ধ্রুবকে মহাকর্ষীয় ধ্রুবক বলা হয়। 

নিউটনের মহাকর্ষ সূত্র অনুসারে,\(F=G\frac{{m_1m_2}}{r^2}\)

এখন\(m_1\)=\(m_2\)=1 এবং r=1 হলে F=G  হয় ।এ থেকে বলা যায়, একক ভরের দুটি বস্তু পরস্পর হতে একক দূরত্বে থেকে পরস্পরের উপর যে পরিমাণ আকর্ষণ বল প্রয়োগ করে তাকে মহাকর্ষীয় ধ্রুবক বলা হয় ।

2)মহাকর্ষীয় ধ্রুবকের i)একক ii)মান ও iii)মাত্রা লেখ  :-

i)মহাকর্ষীয় ধ্রুবকের একক:-

CGS একক:-dyn.cm²g^-2

SI একক:-Nm²kg^-2

ii)মহাকর্ষীয় ধ্রুবকের মান:-

CGS পদ্ধতিতে মান 6.67x10^-8dyn.cm²g^-2

 SI  পদ্ধতিতে মান 6.67x10^-11N.m²kg^-2

iii)মহাকর্ষীয় ধ্রুবকের মাত্রা:- [M^-1L³T^-2]

3)মহাকর্ষীয় ধ্রুবক এবং অভিকর্ষজ ত্বরণের মধ্যে সম্পর্ক প্রতিষ্ঠা কর। 

অভিকর্ষ বলের ক্রিয়ায় অবাধে পতনশীল বস্তুতে যে ত্বরণের  সৃষ্টি হয় তবে তাকে অভিকর্ষজ ত্বরণ বলা হয়। 

 মনে করি m  ভরের একটি বস্তু পৃথিবী পৃষ্ঠের ওপর পৃথিবীর কেন্দ্র থেকে d  দূরত্বে রাখা আছে।  পৃথিবীর ভর M  এর  কেন্দ্রে কেন্দ্রীভূত আছে ধরা যায়।বস্তুটিকে ছেড়ে দিলে অভিকর্ষ বলের প্রভাবে নিচের  দিকে পড়তে থাকে। বস্তুর উপর ক্রিয়াশীল অভিকর্ষীয় বল 

\(F=\frac{GMm}{d^2}\)

এই বলের প্রভাবে  বস্তুতে যদিg  ত্বরণের সৃষ্টি হয় তাহলে লিখতে পারি

\(F=mg\)

\(mg=\frac{GMm}{d^2}\)

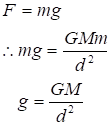\(g=\frac{GM}{d^2}\)........i)

..............i )

বস্তুটি পৃথিবী পৃষ্ঠে অবস্থিত হলে d=R (পৃথিবীর ব্যাসার্ধ )

\(g=\frac{GM}{R^2}\).

4.অভিকর্ষজ ত্বরণ ও পৃথিবীর গড় ঘনত্বের মধ্যে সম্পর্ক  প্রতিষ্ঠা কর। 

মনে করি m ভর সম্পন্ন একটি বস্তু পৃথিবী পৃষ্ঠের উপর পৃথিবীর কেন্দ্র থেকে d দূরত্বে রাখা আছে।

                                                             

 পৃথিবীর ভর  M এর কেন্দ্রে কেন্দ্রীভূত আছে ধরা যায়।  বস্তুটিকে ছেড়ে দিলে অভিকর্ষ বলের প্রভাবে নিচের দিকে পড়তে থাকে ।বস্তুটির উপর ক্রিয়াশীল অভিকর্ষীয় বল

\(F=\frac{GMm}{d^2}\)

 ।এই বলের প্রভাবে বস্তুতে যদি g ত্বরণ সৃষ্টি হয় তাহলে লিখতে পারি 

\(F=mg\)

\(mg=\frac{GMm}{d^2}\)

\(g=\frac{GM}{d^2}\)

এখন পৃথিবীর ব্যাসার্ধ R  হলে

\(g=\frac{GM}{R^2}\)

=\(\frac{G\frac{4}{3}\pi{R^3}\rho}{R^2}\)

=\(G\frac{4}{3}\pi{R}\rho\)

\(\rho=\frac{3g}{4G\pi{R}}\)

এটিই হল পৃথিবীর গড় ঘনত্ব  ও  অভিকর্ষজ ত্বরণ এর  মধ্যে সম্পর্ক।

পৃথিবী পৃষ্ঠ থেকে  i)উচ্চতা  ii)গভীরতা  iii)আহ্নিক গতির জন্য অভিকর্ষজ ত্বরণের  পরিবর্তন -এর জন্য নীল অংশের উপর ক্লিক করো.